2023-03-07

目標までの距離をもとに放物線の最適な発射角度を求める計算方法

プログラミング・ゲーム作り

ゲームにはさまざまな武器が登場するが、
銃弾は直線的な軌道として処理することが多い。

現実には弾丸も重力の影響を受けて放物線を描くのだが、
一般的なイメージとして銃の弾が徐々に落下するという印象が薄いし、
そこまで計算して敵に狙いをつけるのは
ゲームとしての面白みに欠けるからだ。

しかし、戦車砲やグレネードランチャー、弓矢などは
山なりに飛んでいく印象が強いため、
重力を無視して飛ばしてしまうと不自然に見えてしまう。

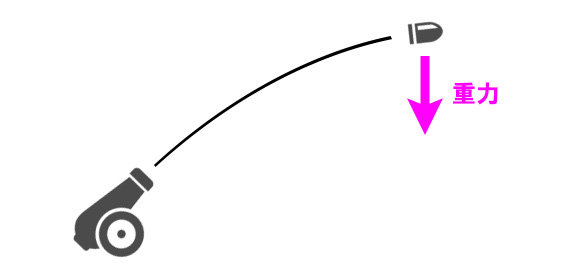
そこで発射された弾は、重力によって
徐々に下に落ちていくように処理する。

移動量は２つに分解して処理する

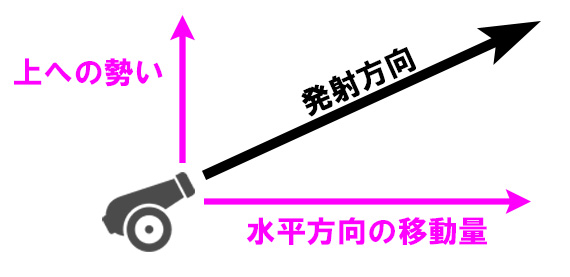
プログラム的には垂直方向の移動処理と
水平方向の移動処理を別々に管理した方が楽なので、
発射時の角度をもとに三角関数を使って
移動量を水平方向と垂直方向に分解する。

このうち水平方向の移動量は減衰せず、
毎回同じ分だけ弾の座標に足し込んでいく。
空気抵抗を考えても誰も得しないので普通は無視する。

垂直方向の移動量は徐々に減少していって
いずれマイナス値になるのだ。
つまり、弾は下降していくことになる。

さて、主人公が発射する武器はプレイヤーが操作をするので
発射時の向きに合わせて弾を飛ばすだけでいい。
弾の着弾位置から発射方向を修正する作業がゲーム性につながる。

問題は敵が弾を発射する場合だ。

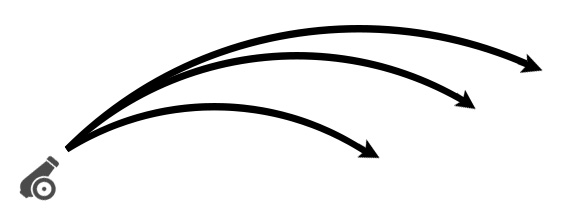
敵はプレイヤーが操作するわけではないので
主人公にうまく当たるように弾を撃たせる必要があるが、
発射する角度によって弾の飛距離が変わるので、
目標までの距離に応じて角度を求める必要がある。

しかし重力によって垂直方向の移動量が変化するため
どんな角度で撃ち出せば
ちょうど目標地点に落ちるかという計算はなかなか難しい。
今回はこの計算方法を紹介してみる。

着弾するまでの滞空時間を求める

まず手順としては、弾が地面に着くまでの時間を求める。
そのために垂直方向の移動量を抜き出す必要があるが、
これには三角関数を使う。

直角三角形の角度と斜辺の長さがわかれば
コサインを使って底辺の長さとを求めることができる。

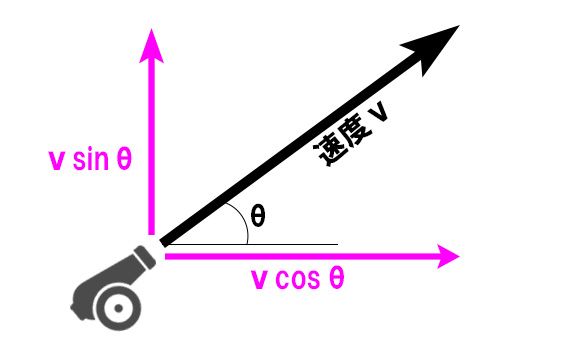
つまり、角度θの方向にｖの速度で発射された弾は
水平方向にｖ×コサインθ 、
垂直方向にｖ×サインθ の力で撃ち出された考えられる。

次に高校物理で出てくる等加速度運動の公式を使う。

上方向をプラスとした場合、
初速度 ${v_0}$ 、重力加速度 ${g}$ に対する時間 ${t}$ のときの高さ ${y}$ は

　 ${\displaystyle\ y=v_0 t-\dfrac{1}{2}\ gt^2 }$

となるので、この ${v_0}$ に
先ほどの垂直方向の発射速度 ${vsin\theta}$ を当てはめると

　 ${\displaystyle\ y=vsin\theta\ t-\dfrac{1}{2}\ gt^2 }$

になる。

弾が地面に着くということは ${y}$ が ${0}$ になるときなので

　 ${\displaystyle\ 0=vsin\theta\ t-\dfrac{1}{2}\ gt^2 }$

になるときの ${t}$ の値を求めればいいわけだ。

この式を並び替えると

　 ${\displaystyle\dfrac{1}{2}\ gt^2\ -vsin\theta\ t+0=0}$

となり、２次方程式の

　 ${\displaystyle\ ax^2\ +bx+c=0}$

と同じ形になる。
${x}$ が ${t}$ 、 ${a}$ が ${\dfrac{1}{2}\ g}$ 、 ${b}$ が ${-vsin\theta}$ 、 ${c}$ が ${0}$ ということだ。

２次方程式なら中学数学で習う

　 ${\displaystyle\ x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$

解の公式が使える。

この式にそれぞれを当てはめると

　 ${\displaystyle\ t=\dfrac{-({-vsin\theta})\pm\sqrt{({-vsin\theta})^2-4\times{\dfrac{1}{2}\ g}\times\ 0}}{2\times{\dfrac{1}{2}\ g}}}$

となるが、これを整理していくと

　 ${\displaystyle\ t=\dfrac{{vsin\theta}\pm\ {vsin\theta} }{g}}$

と、かなりシンプルにすることができて

　 ${\displaystyle\ t=0 , \biggl( \dfrac{2\times{vsin\theta}}{g}\biggr)}$

±の関係で２つの解が出る。
つまり弾の高さが０になる時間は ${0}$ と ${\biggl(\dfrac{2\times{vsin\theta}}{g}\biggr)}$ ということだ。

このうち時間 ${0}$ というのは発射の瞬間を表しているので、
発射角度 ${\theta}$ における着弾までの時間は

　 ${t=\dfrac{2\times{vsin\theta}}{g}}$

となる。

サイン値が最大となるのは90度なので
${\theta}$ が90に近づくほど ${t}$ の値も大きくなる。
要するに、上向きに撃つほど
滞空時間が長くなるという納得の結果になっている。

滞空時間をもとに飛距離を求める

角度θの方向にｖの速度で発射された弾は
水平方向にはｖ×コサインθ だけ進む。
こちらは重力には左右されないので速度は変化しない。

等速運動の移動量は等加速度運動の公式である

　 ${\displaystyle\ x=v_0 t+\dfrac{1}{2}\ at^2 }$

の加速度 ${a}$ が ${0}$ になっている状態なので、

　 ${\displaystyle\ x=v_0 t}$

となるが、この ${v_0}$ の部分に ${vcos\theta}$ を当てはめれば

　 ${\displaystyle\ x=vcos\theta\ t}$

となり、弾が水平方向に対して
どのぐらい移動するかを求めることができる。

この式の ${t}$ に先ほど求めた滞空時間 ${\biggl( \dfrac{2\times{vsin\theta}}{g}\biggr)}$ を当てはめれば

　 ${\displaystyle\ x=vcos\theta\times\dfrac{2\times{vsin\theta}}{g}}$

となり、少し式を整理すると

　 ${\displaystyle\ x=\dfrac{cos\theta\sin\theta\times\ 2\times\ v^2}{g}}$

という形になる。

三角関数の加法定理に

　 ${\displaystyle\sin( \alpha\ + \beta\ )=sin \alpha\cos \beta\ +cos \alpha\sin \beta}$

があるが、 ${\alpha\ = \beta}$ の場合に置き換えてみると

　 ${\displaystyle\sin( \alpha\ + \alpha\ )=sin \alpha\cos \alpha\ +cos \alpha\sin \alpha}$

となり、

　 ${\displaystyle\sin(\alpha\times\ 2 )=cos \alpha\sin \alpha \times\ 2}$

とすることができる。

ということは先ほど作った式、

　 ${\displaystyle\ x=\dfrac{cos\theta\sin\theta\times\ 2\times\ v^2}{g}}$

の「 ${\cos\theta\sin\theta\times\ 2}$ 」の部分を
そっくり「 ${\sin(\theta\times\ 2)}$ 」に置き換えることができるので、

　 ${\displaystyle\ x=\dfrac{\sin(\theta\times\ 2)\times\ v^2}{g}}$

という式になる。
これが角度 ${\theta}$ で弾を発射したときの飛距離だ。

放物線で移動する物体は高さと推進力のバランスから
45度で発射されたときが一番よく飛ぶわけだが、
上記の ${\theta}$ に45が入ると、サイン値の最大である
90度が使われるようになっているのがわかる。

また、発射速度 ${v}$ が大きくなれば飛距離 ${x}$ が増え、
重力加速度 ${g}$ が大きくなれば飛距離 ${x}$ が小さくなることからも
計算として正しいことが感覚的にわかるだろう。

45度で発射したときの飛距離より遠くには
どう撃っても絶対に弾は届かないので、
敵のAI処理ではまず上記の式の ${\theta}$ に45を代入して射程距離 ${x}$ を求め、
目標がそれより近いときだけ攻撃するようにすべきだ。

飛距離から逆算して発射角度を割り出す

さて、目標が射程範囲内にいる場合は
適切な発射角度を求めて攻撃する必要があるため、

　 ${\displaystyle\ x=\dfrac{\sin(\theta\times\ 2)\times\ v^2}{g}}$

先ほどたどり着いたこの式を少し変形して

　 ${\displaystyle\ sin(\theta\times\ 2)=\dfrac{xg}{v^2}}$

左辺にサイン値がくるようにする。
これを見ると ${\dfrac{xg}{v^2}}$ がサイン値と等しいことがわかる。

角度からサイン値を求める場合はサイン関数を使うが、
サイン値から角度を求める場合は
サインの逆関数であるアークサインを使う。

　 ${\displaystyle\theta\ = arcsin(\dfrac{xg}{v^2})\div\ 2}$

ようやくたどり着いた。
これが目標との距離 ${x}$ 、重力加速度 ${g}$ 、発射速度 ${v}$ をもとに
適切な発射角度を割り出す計算式となる。

ここまでたどり着くのに

三角関数
等加速度運動
加法定理
解の公式
逆三角関数

といった数学知識を活用する必要があり、
中学高校での勉強が大切なことを実感する。

実践での工夫

もともとこの処理は18年ほど前に作った
自作ゲーム「ネイビーミッション」で
艦砲射撃をしてくる敵の攻撃AIとして必要だったのだ。
当時はかなり四苦八苦して上記の結論に達したのを覚えている。

さらに後半のステージで登場する強めの敵では
途中に出てきた発射角度から滞空時間を求める式

　 ${t=\biggl( \dfrac{2\times{vsin\theta}}{g}\biggr)}$

を使って、敵弾が飛んでいる間に
自機が進むであろう位置を先読みして
未来の座標に向けて発射するようにもした。

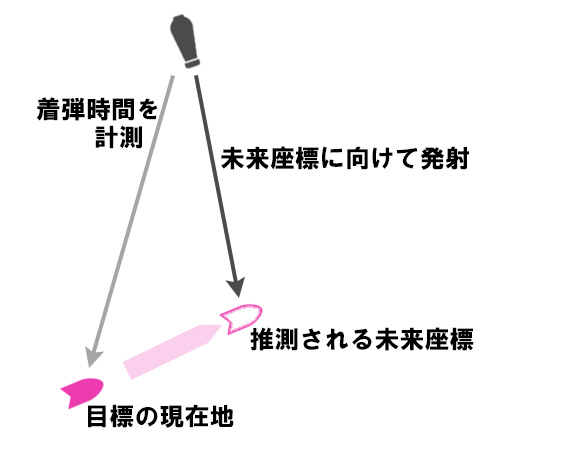
いわゆる偏差（へんさ）射撃というやつだが、これによって
「とりあえず移動していれば当たらない」という序盤の敵に対して
「攻撃してきたら移動方向を変えないと喰らう」という強敵が作れた。

開発中にややこしい計算をした感触だけは覚えていたので
当時の資料を掘り起こしてきちんと記録にまとめてみた。
（数式をブログ上で表現するTeX記法の練習にもなった）

同じような計算が必要になるプログラマーに
少しでも役立てばと思う。

mclover.hateblo.jp

2023-03-01

2023年に観た一番エグい映画は「神は見返りを求める」

reblog.hateblo.jp

観たときにどうしようもなく嫌な気持ちになる映画を
「エグい映画」と称して探し求めている。

わざわざ嫌な気持ちなんか味わいたくないと思うかもしれないが、
絶叫マシンに乗りたい気持ちと似ていて
スリリングな状況にヒヤヒヤする感覚と
「よくこんな嫌なこと思いつくなぁ」という刺激がたまらないのだ。

2023年が始まって間もないが、
先日観た「神は見返りを求める」はおそらく今年一番の収穫だ。

底辺YouTuberが作る企画の絶妙にヌルい感じと
人気が出てどんどん調子に乗っていく様子がめちゃくちゃリアルで、
それを善意で支える中年男性が
プライドをズタズタに傷つけられて暗黒化していく流れも強烈。

主役２人を演じる岸井ゆきのとムロツヨシの振れ幅が凄まじくて、
「人間こんなにも変わるものなのか」と思わせられる。
この作品は登場人物全員がイヤな奴なのだが、
それでいて「こういうヤツいるよなー」のオンパレードなのが怖い。

ほのぼのするのは最初の30分だけで、
それ以降は観ている側をどんどんイヤな気持ちにさせてくるし、
「もう勘弁して」と思ってるのにまったく追撃が止まらない。

YouTuberたちが醸し出す雰囲気とか
配信する動画の「いかにも」な造りがやたらうまくて、
常時ヘラヘラしているノリや
人気を得るためにエスカレートしていく様子もリアルすぎる。

なりたい職業ランキングでも上位に挙がるYouTuberだが、
子供が「ユーチューバーになりたい」と言い出したら
とりあえず本作を見せて覚悟を決めさせるといいんじゃないかな。

今ならAmazonプライムビデオで観れるので
そのエグさに耐えられるならぜひ観て欲しい。

ちなみに今年観たエグい映画の次点は「岬の兄妹」。
こっちはこっちで種類の違うダメージを与えてくる衝撃作だった。

これまでのエグい映画まとめ

2010年「告白」
2011年「ブラック・スワン」
2012年「冷たい熱帯魚」
2013年「縞模様のパジャマの少年」
2014年「ドッグヴィル」
2015年該当なし（次点「灼熱の魂」）
2016年「怒り」
2017年該当なし
2018年該当なし
2019年「スリーピングタイト」
2020年「獣道」
2021年「誰も知らない」
2022年「我々の父親」
2023年「神は見返りを求める」

2023-02-27

水曜日のカンパネラのボーカルが机の下で踏むステップがうますぎた

オススメ動画

音楽ユニット「水曜日のカンパネラ」が歌う
「エジソン」という曲のミュージックビデオでは
ボーカルの詩羽（うたは）がリズムに合わせてステップを踏むのだが、
これがめちゃくちゃにうまくて
初めて観たときに衝撃を受けた。

何かダンスでも習っていた人なのかと思ったが、
映像の最後で明かされるように
実は下半身だけダンサーのものを合成しているのだった。

それにしてもプロの技のスゴさを見せつけられた。リズム感抜群。

2023-02-22

今後起きる問題は未来の自分が悩むはずだと割り切ってしまう

自己成長の考え方

明日のことまで思い悩むな。
明日のことは明日自らが思い悩む。
その日の苦労は、その日だけで十分である

―――「新約聖書」マタイによる福音書６章34節より

学生と話をしていると、
とにかく自信がなくて今後が不安で
悶々と思い悩む傾向が強いように感じる。

悩むのは別に構わないのだが、
問題は不安がどんどん膨らんで
自分が出せる勇気の量を上回り、
何も行動できなくなってしまうことだ。

そうなると失敗を恐れる行為そのものが
実際に失敗を招くという悪循環に陥ってしまい、
悩んでいることがマイナスに働いてしまう。

今後起きる問題は未来の自分が悩むはずだと割り切って
とりあえず今できることをやっていく方が有益だ。

mclover.hateblo.jp

2023-02-16

ノートパソコンのフタにあるメーカーロゴが逆向きになった日

ノートパソコンのモニター裏、つまりフタになっている部分には
たいてい製造メーカーのロゴが刻まれているが、
ノートパソコンが普及し始めた当初は今と逆向きで
フタを閉じたときに利用者に正対する形になっていた。

ノートパソコンといえばそれが普通だったのだが、
ある世代の製品で急にロゴが逆向きのものが登場したのだ。
私は職業柄、毎年新しいノートパソコンを目にするが、
ロゴが逆になったことに気づいたのは2000年代のVAIOだったと思う。

初めて見たときはかなり違和感があった。
いざパソコンを使おうとフタに手をかけると
自分に対して逆方向を向いたロゴが目に入るからだ。

これは、１人しかいない利用者に正しい向きを見せるより
周囲を行き来する多くの人々にロゴを主張した方が
メーカーを印象付けることができるという判断なのだろう。
実際、映画やドラマでパソコンが出てくるときには
今の向きの方がしっかりロゴが映って宣伝できる。

スマートフォンをはじめ、たいていのデバイスは
利用者もそれを眺める周囲も同じ向きでロゴを眺めるが、
ノートパソコンだけはそれが逆になるという
珍しい存在であることに気づかされる革新だった。

プチメタ3.0

刺激を受けた物事に対する感想や考察、資産運用や英語学習、自己成長に関することなど。