
対戦型の3Dゲームなどで
主人公と敵が常に画面に収まるよう、
カメラの距離を自動で調整したいことがある。

一番遠い距離で固定してしまうと
両者が接近したときに迫力がなくなるため、
離れているときだけ遠くから映し、
接近戦ではカメラを寄せるようにしたいわけだ。
格闘ゲームではよくある表現だが、
これを実現しようと思うと数学が絡んでくる。
カメラが見ている上下の距離を割り出す
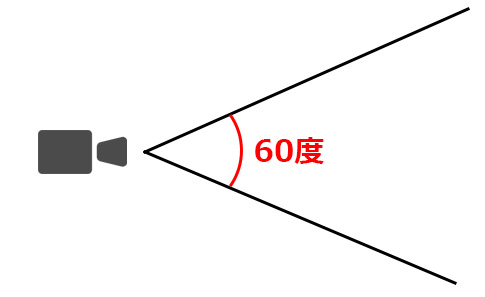
3D世界を映すカメラの画角は自由に設定できるが、
これは一般的に縦方向の角度である(今回は60度とする)。
ゲーム画面は横長なので水平方向の画角はもう少し広くなる。
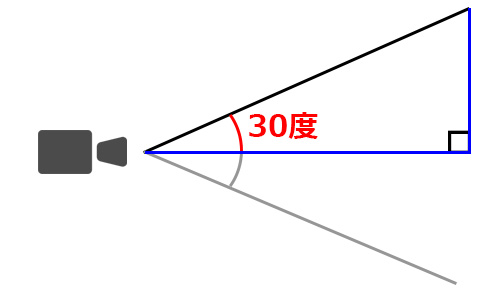
縦方向の画角を上半分だけで考えると30度になり、
カメラから前方に伸ばした直線を底辺とした
直角三角形をイメージすることができる。
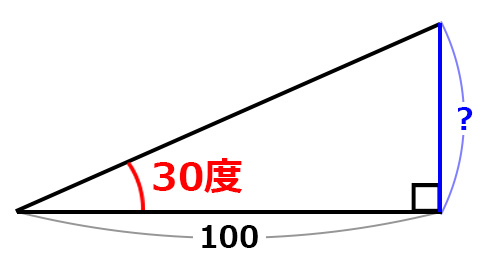
たとえば底辺の長さが100だった場合、
この直角三角形の高さはいくらになるか。
これは三角関数のタンジェントで求めることができる。
これにより、三角形の高さは約57だとわかる。
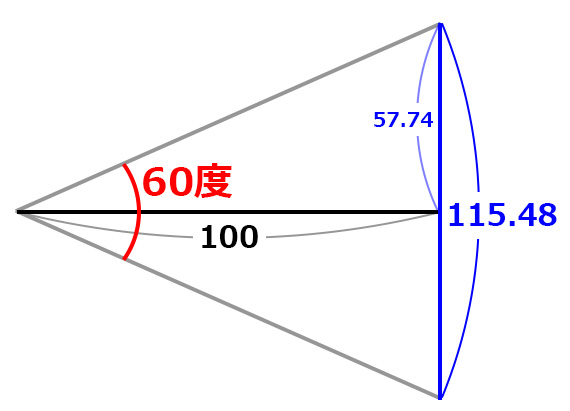
この三角形が上下につながっているわけだから
ある場所から100離れたカメラが見渡している
上下方向の距離は約115ということだ。
カメラの水平方向の画角を求める
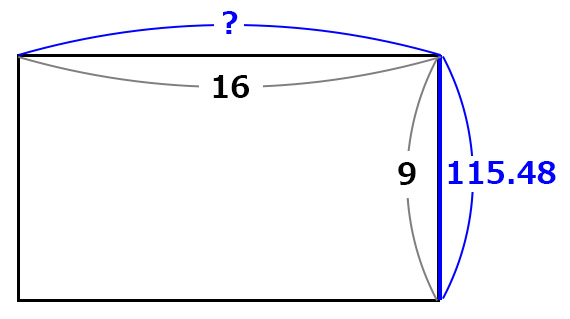
普通、ゲーム画面は横長サイズなので
縦方向に見渡せる範囲より横方向の方が広い。
一般的には16:9という比率(アスペクト比)になっているので
という計算で水平方向に見渡している距離がわかる。
ここから逆算する形でカメラの水平方向の画角を求める。
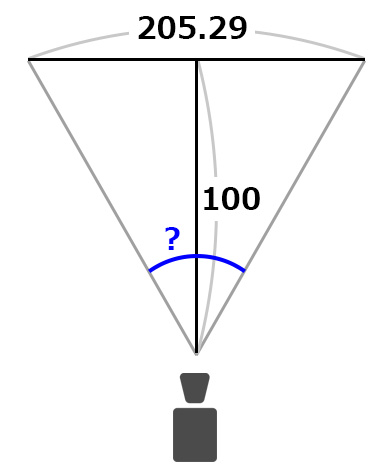
これまでの内容をまとめると
ある場所から100離れたカメラが見渡している
左右方向の距離は約205ということだ。
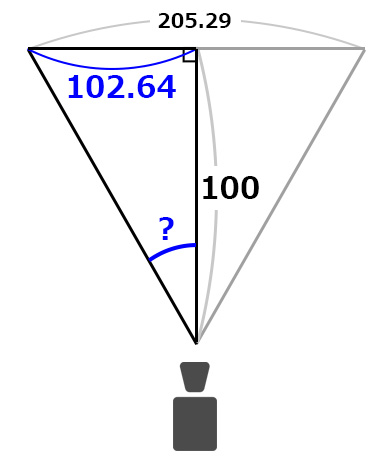
ここで直角三角形を見つけられるとベストだ。
右に90度回転して考えるとわかりやすいが、
底辺の長さが100、高さが約102の直角三角形になっている。
この2辺の長さから角度を割り出すには
タンジェントの逆関数であるアークタンジェントを使う。
実際には100倍や2倍する必要はないので、
とすれば一気に計算できる。
これは左半分の角度なので左右の画角では約91度になるが、
今後の計算の中では45度の方を使う。
キャラクターを頂点とする二等辺三角形を考える
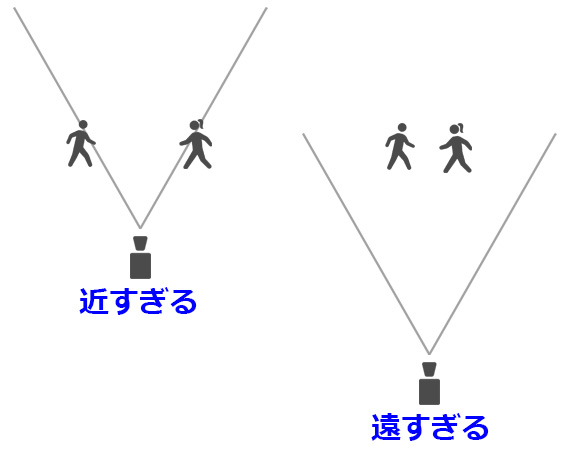
カメラの画角は一定なので、
キャラクターをうまく視界に収めるには
対象者との距離で調整する必要があるわけだ。
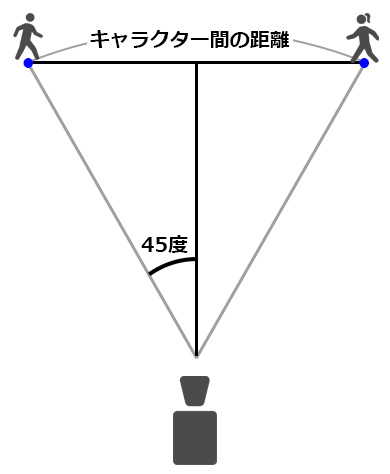
2つのキャラクターがはみ出さないようにするには
両者を結んだ直線を底辺とする二等辺三角形をイメージすればよい。
(実際にはキャラクターのやや外側に頂点を置く方が綺麗)
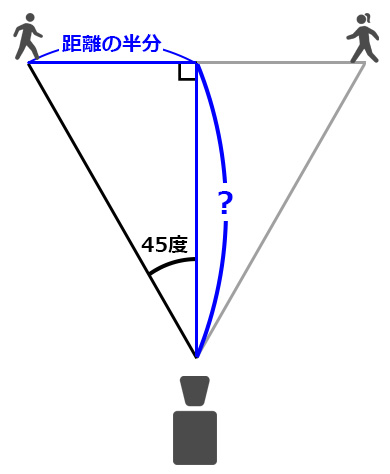
ここでも直角三角形を見つけられただろうか。
とにかくゲームプログラミングは三角関数に頼る部分が多い。
今回も右に90度回転して考えるが、
キャラクター間の距離の半分を高さとする45度の直角三角形で、
この底辺の長さがカメラの理想的な距離というわけだ。
タンジェントというのはもともと
と定義されているわけだから、これを変形すれば
底辺の長さ=高さ ÷
となり、今回の値を当てはめれば
理想的なカメラ距離=キャラ間の距離の半分 ÷
となる。
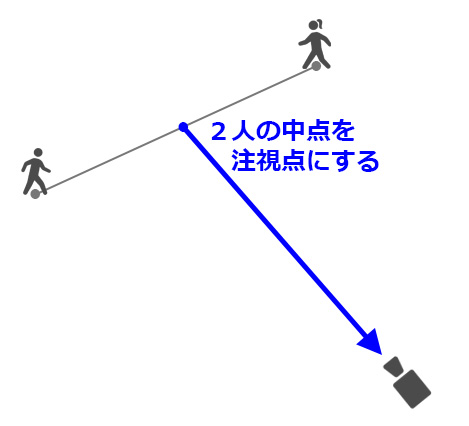
あとは2つのキャラクターのちょうど中間の座標を
注視点(カメラが見ている場所)に設定し、
そこから理想距離だけ離した場所にカメラ本体を置けばいい。
市販ゲームで使われている処理も
実は中学数学さえわかれば実現できたりする。