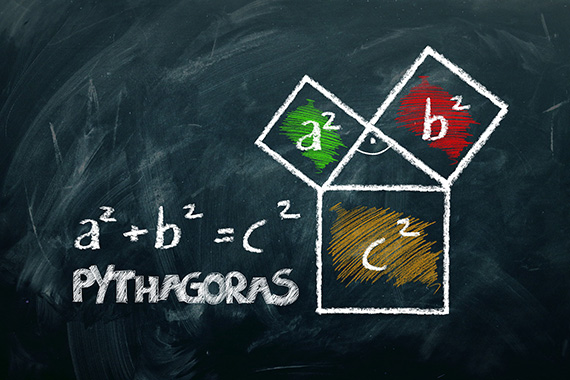
中学校の数学で習う「三平方の定理(ピタゴラスの定理)」は
ゲーム開発の中でも使われまくっている。
この理屈がなければあちこちが破綻するほどなので
先日紹介した三角関数以上に重要なものだと思っている。
三平方の定理とは

そもそも三平方の定理とは
直角三角形における3つの辺の長さの関係を表したものだ。
直角三角形の底辺の長さと高さをそれぞれ2乗し、
それらを合計した値の平方根は、斜辺の長さに等しい。
斜辺の長さだけに限らず、式を組み替えれば
どの2辺からでも残り1辺の長さを求めることができる。
「長さを知りたいなら直接測ればいいのに」と思うかもしれないが、
縦の長さや横の長さは簡単に測れても
斜め方向はそうはいかないことが多いのだ。
2点間の距離を求める
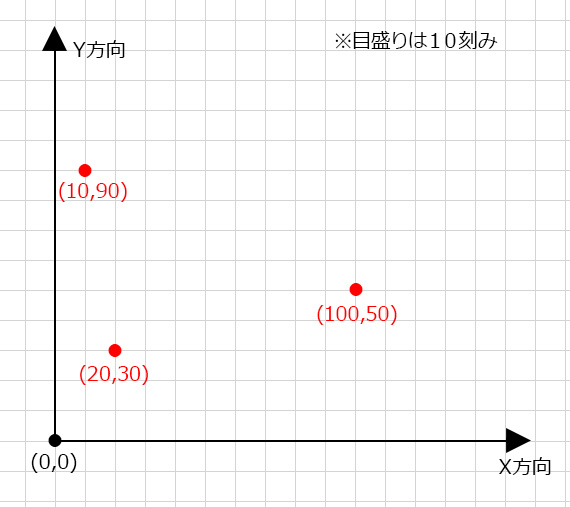
基本的にプログラムで表示する物体の位置は
横方向を表すX座標と縦方向を表すY座標で管理されている。
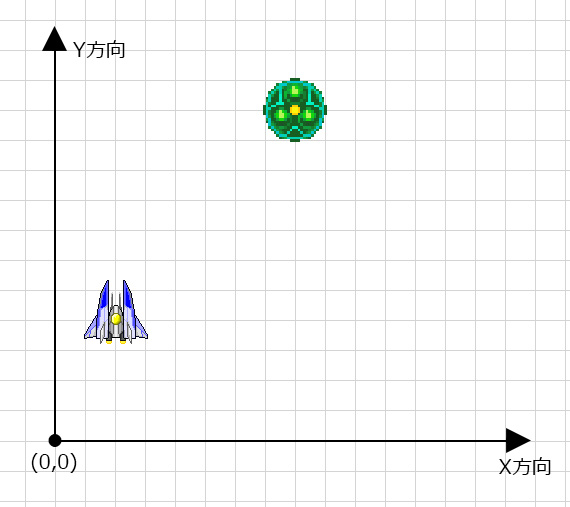
つまりゲームに登場するキャラクターが
表示されている位置は簡単にわかる。
ではこの2つのキャラクターが
どれぐらい離れているかという「距離」は
どうすれば求められるだろうか。
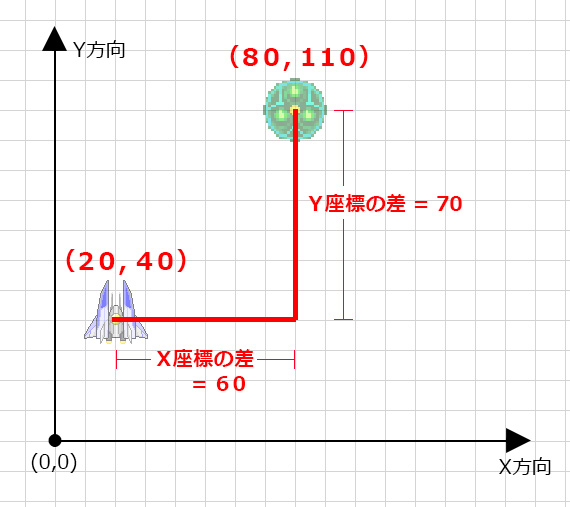
それぞれのキャラクターはXY座標を持っているので
X座標同士を引き算すれば横方向の離れ具合が、
Y座標同士を引き算すれば縦方向の離れ具合がわかる。
この2つの数値を直角三角形の底辺と高さに見立てれば
キャラクターを結ぶ直線が斜辺となるのだ。
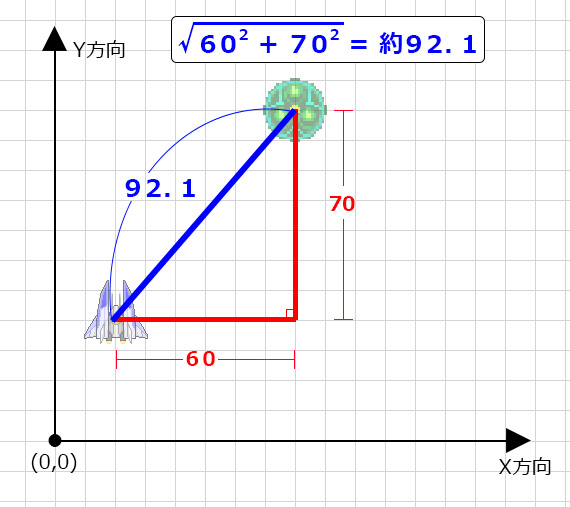
あとは三平方の定理に当てはめれば
斜辺の長さ、つまりキャラクター間の距離が求まる。
この「2点間の距離を求める」という作業が
三平方の定理のもっとも基本的な利用法である。
当たり判定に利用する
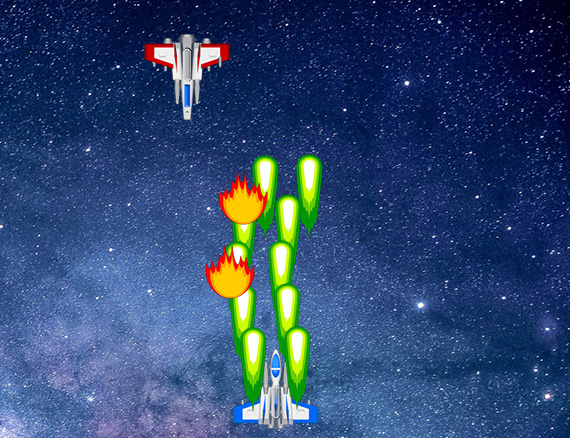
ゲームでは「自機が敵とぶつかったか」
「自機がアイテムを取ったか」「弾が敵に当たったか」といった
2つの物体が衝突したかを判定したいことが非常に多い。
こういった処理は「当たり判定(衝突判定)」と呼ばれる。
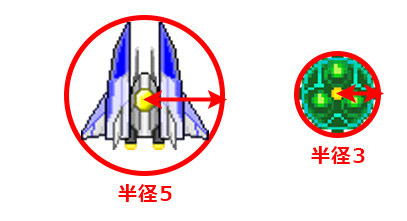
当たり判定を実現するには
まず各キャラクターが収まる円を想定する。
キャラクターによって大きさが違うので
それぞれに見合った半径の円を考える。
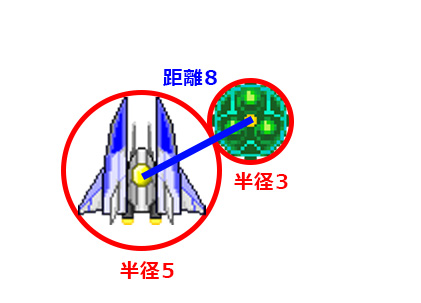
半径5と半径3のキャラクターは
互いの距離が8のときにギリギリ触れる状態になり、
これ以上近い場合はめり込んでいることになる。
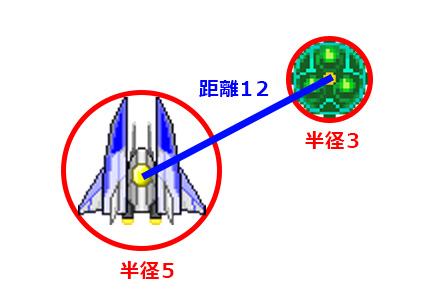
互いの距離が12のときは4離れているというわけだ。
つまり2つのキャラクターの「距離」と「半径の合計」を比べれば
衝突しているかどうかがわかる。
これが距離による当たり判定(円判定)だ。
それぞれのキャラクターに合わせて半径を設定しておけば、
「敵と敵」「アイテムと自機」「弾と自機」など
どういった組み合わせであっても
どのぐらいの距離で衝突することになるかがわかる。
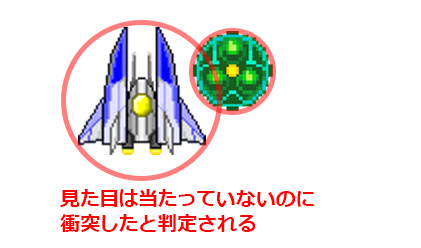
問題としては単なる円として判定しているため、
実際のグラフィックでは衝突していないように見えても
円同士が触れていると当たっていることになってしまうことだ。
これだと理不尽だと受け取られることが多く、
ゲームを遊んでいるプレイヤーから不満が出てしまう。
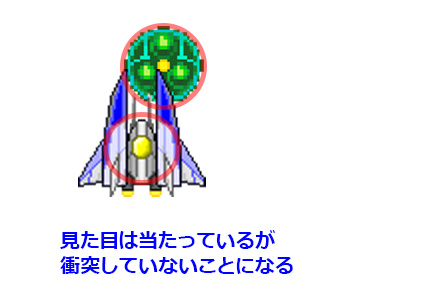
そこでグラフィックよりも小さめの円に設定することが多い。
今度は逆に、見た目では重なっているのに
内部では衝突していないと判定されてしまうが、
プレイヤーは自分にメリットがある場合は
ほとんど不満を言わないので問題視されない。
目的地に近づく処理に利用する
別の利用法も挙げてみる。
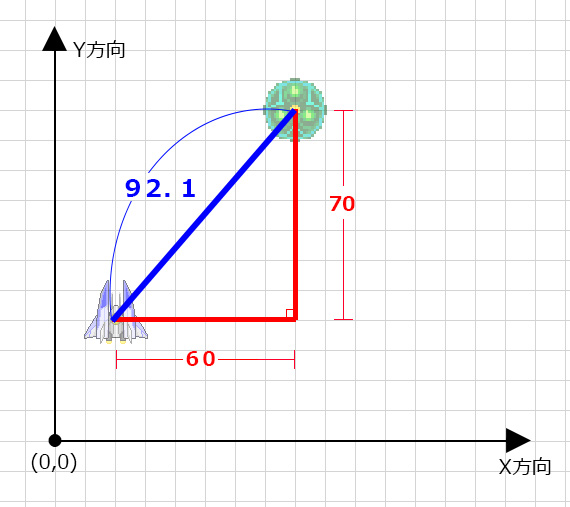
先ほどと同様に2つの座標の距離を求めるが、
片方を「現在地」、もう片方を「目標地点」と考える。
水平方向に60、垂直方向に70離れているので
目標地点までの距離は92.1だとわかる。
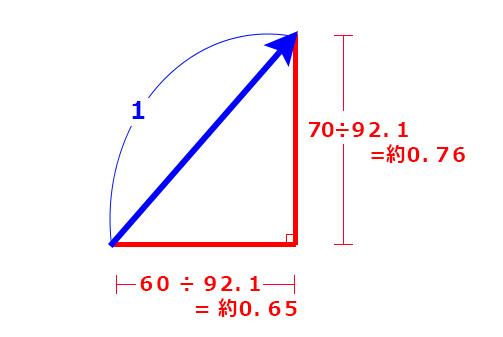
さて、この目標地点までの距離で
水平方向の長さ、垂直方向の長さを割ると、
目標方向に1近づくためには
XY座標にいくつ足せばいいのかという値がわかる。
これを使えばあるキャラクターが
指定した座標に少しずつ近づく処理が作れる。
移動量を2倍すれば2ずつ、3倍すれば3ずつ近づいていくので
好きな速度で移動するキャラクターを作ることができるわけだ。
自分で考えるより公式を知っている方が楽
数学の公式を覚えるのを嫌がる人が多いが、
優秀な数学者たちが苦労して編み出した理屈に
自力でたどり着ける可能性はほとんどないわけだから
公式を知らずに必死で考えるよりも覚えた方が楽だ。
ゲームプログラミングには数学が必須と言われるが、
最低限、三平方の定理と三角関数は押さえておきたい。