
「三角関数なんて何の役に立つの?」というのは
勉強にウンザリした中高生がよく言うセリフだが、
実はめちゃくちゃに利用価値の高い理屈なので
意識しないだけでそこらじゅうに使われている。
当然、ゲーム作りにおいても大活躍しているので
そのあたりを解説してみようと思う。
キャラクターの位置はXY座標で管理される
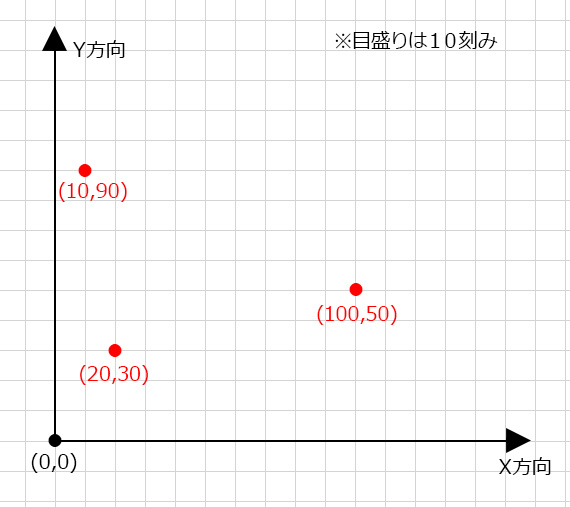
まず物体の位置を表す数値として
「座標」が使われていることを知る必要がある。
座標とは、ある場所を基準にして
そこからどのぐらい離れているかを表す数値だ。
よく使われるのは縦横2方向の距離を使う「直交座標 *1 」だろう。
横方向の位置を「X座標」、縦方向の位置を「Y座標」と呼び、
基準点から右方向に5、上方向に3離れていれば(5,3)と表現する。
地球上の位置を表す東経や北緯も考え方は同じである。

ゲーム中に表示される画像の位置は
この座標で管理されているので、
キャラクターを移動させるときはXY座標を変化させる。
速いスピードで移動させたければ
座標に大きな値を足し引きすればいい。
ここで問題となるのがナナメ移動だ。
縦か横にまっすぐ移動するだけなら
XY座標のどちらかを増減させるだけで済むが、
ナナメに移動させるなら両方を変化させる必要がある。
しかし希望の角度に移動するために
2つの数値をどの程度変化させるのかが難しい。

「45度の方向なら簡単」と思うかもしれないが、
単純に横移動や縦移動のときと同じ量を
XY座標の両方に足してしまうと
ナナメ移動のときだけ大きく移動してしまう。
これは古いゲームで実際に起こっていた問題だ。
このあたりを解決してくれるのが三角関数である。
サイン・コサインとは直角三角形の辺の長さ

代表的な三角関数はサイン・コサイン・タンジェントだが、
簡単に言えば斜辺の長さが1の直角三角形において
三角形の高さが「サイン」、底辺の長さが「コサイン」である。

斜辺の長さが同じ1でも、直角三角形の角度によって
高さと底辺の長さは変化する。
角度が90度に近づくほど三角形は高く、底辺は短くなり、
角度が0度に近づくほどその逆の変化になる。

いつ調べても三角形の形や大きさは変わらないわけだから
すべての角度におけるサイン・コサインは決まっている。
指定した角度におけるサインを求めるのがサイン関数、
コサインを求めるのがコサイン関数だ。

また、サインやコサインの値は、関数電卓や
iPhoneを横向きにしたときの電卓でも求めることができる。
(サイン30度なら「30」を押してから「sin」を押す)
ナナメ移動にサイン・コサインを利用する


斜辺の長さが1の直角三角形を基準とすれば、
それより大きな三角形の高さや底辺の長さも
サインやコサインに倍率をかければ求めることができる。

その理屈を使えば、好きな角度に好きな量だけ移動できる。
X座標に「コサイン × 移動量」、
Y座標に「サイン × 移動量」を足せばいいのだ。
コサイン30度は0.87、サイン30度は0.5なので、
30度方向に70移動させたい場合は
X座標に「コサイン30度(=0.87)× 70」で61、
Y座標に「サイン30度(=0.5)× 70」で35を足せば
縦横の移動量がちょうど合わさってナナメ移動する。
また、コサイン90度は0、サイン90度は1なので、
90度方向(まっすぐ上)に50だけ移動する場合も
X座標に「コサイン90度(=0)× 50」、
Y座標に「サイン90度(=1)× 50」を足すので
実質的にはY座標にのみ50を足したのと同じ結果になる。
こういった理屈を使えば
敵キャラがいろいろな方向に弾を発射する
弾幕シューティングのような表現も可能になる。
タンジェントを応用すると角度を求められる

サイン・コサインとセットで登場する「タンジェント」は
直角三角形の高さを底辺の長さで割ったものだ。
つまり底辺に対して高さが何倍あるのかという比率を表す。
たとえば45度の直角三角形なら
高さと底辺は同じ長さなのでタンジェントは1だ。


「比率」ということは、三角形の大きさが変わっても
角度さえ同じならタンジェントの値は変わらない。
つまり、タンジェントがわかれば角度が決まるのだ。

タンジェントも角度ごとにすべて決まっているので
一覧表を作ることができる。
角度をもとにタンジェントの値を求めるのがタンジェント関数だ。

タンジェントが役立つのは特定の物体を狙うような処理だ。
自機を狙って発射される敵の弾や
目標に対して進んでいく誘導ミサイルなど、
ある場所に向かってナナメ移動させたいことがある。

2つのキャラクターに直角三角形を当てはめてみると、
底辺の長さはX座標の差、
高さはY座標の差になることがわかる。
高さと底辺の長さがわかればタンジェントが計算できるので
それがどの角度の三角形に当てはまるのかを探す。
そのためには、タンジェント関数とは逆に
タンジェントの値から角度を求められるアークタンジェント関数を使う。

たとえばX方向に60、Y方向に80ズレている場合、
タンジェントは「80÷60=1.3」となり、
それに当てはまる角度は約53度であることが求まる。
あとは前述したサイン・コサインを使ってその角度に移動させれば
目標に向かって近づいていくキャラクターが表現できる。
まとめ
三角関数の利用場所はかなり広く、
上記で解説したのは一番基本的な使い方だが、
これだけでも三角関数が必須であることがわかるだろう。
そう言うと数学が得意でなければ
ゲーム開発ができないように思うかもしれないが、
中学高校で習う数学の中でもかなり部分的にしか利用しないので
いざ必要になったときにポイントを押さえて学習できれば十分。
大切なのは数学に対する拒絶感を持たないことと、
必要なことを自分で調べて習得できる独学能力だ。
*1:角度と距離を使った「極座標」という考え方もある