
ボールや車両、魔法や敵キャラなど
ゲームの中で何かを壁面に反射させたいことがある。
水平と垂直の壁しかないような2Dゲームなら
進行方向を表す角度をうまく計算するだけでも大丈夫だが、
いろいろな向きの壁が存在したり
3D空間内を移動動するような場合ではもう少し別の方法を使う。
法線
正しい反射処理を実現するためには
「法線(ほうせん)」を理解しておく必要がある。
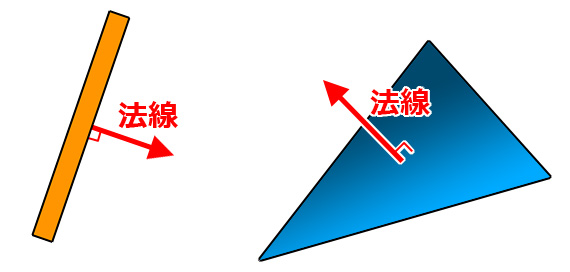
法線とは壁面に対して垂直に伸びるベクトルのことで、
3Dプログラミングの場合は
ポリゴン面の表側に立っているイメージだ。
簡単に言えば「面の向き」を表しているのだが、
ゲームプログラミングでは
法線をうまく利用した処理がたくさんある。
物体は移動ベクトルに従って進むようにする
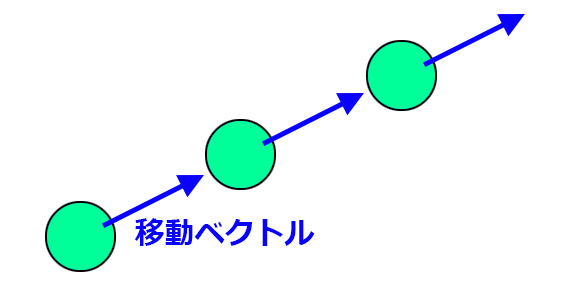
キャラクターが移動する場合は
「そのキャラが向いている方向に前進する」という処理を作るが、
「壁に跳ね返る」というのは外的要因なので
その物体がどっちに向いているかは関係がないため、
単純に絶対方向を表す移動ベクトルに従って動かす方がよい。
つまり、(3,0,0)というベクトルなら3D空間の右方向に、
(-2,2,0)なら3D空間の左上方向に移動するわけだ。
入射角と反射角を等しくする必要がある
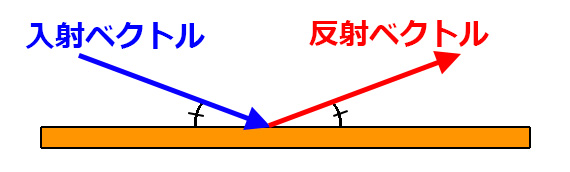
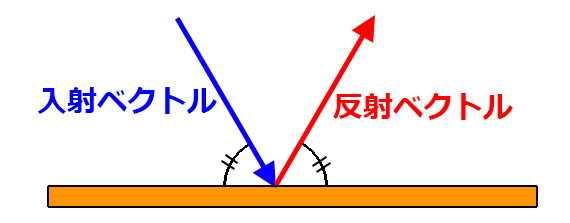
中学や高校で習う光の反射の法則と同様、
自然な跳ね返りに見せるには
壁面にぶつかった角度と同じ角度で出ていく必要がある。
移動ベクトルによって進んでいる物体の場合は
入射ベクトルが壁と衝突する前の移動ベクトルで、
反射ベクトルが新たな移動ベクトルということだ。
ベクトルの内積を使って長さを求める
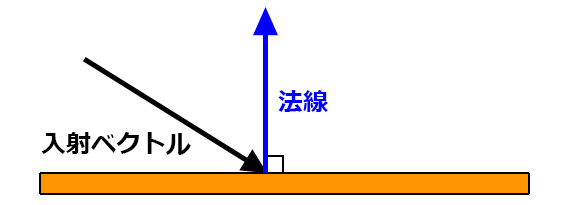
正しい反射ベクトルを求めるには
まず物体が衝突した壁面の法線が必要になる。
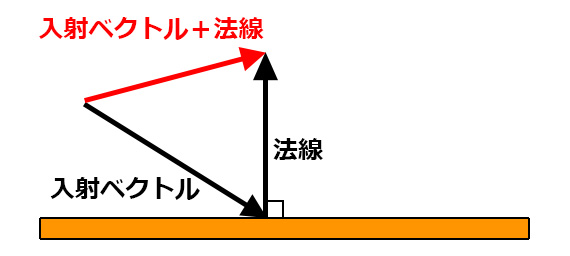
ベクトル同士は足し算することができるので、
たとえば入射ベクトルと法線(ベクトル)を足すと
片方の末端からもう片方の先端を結んだベクトルが求まる。
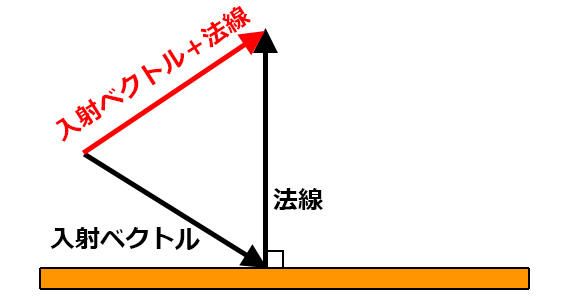
もし法線が長ければ
2本のベクトルを足した結果は
かなり上を向いたベクトルになるし、
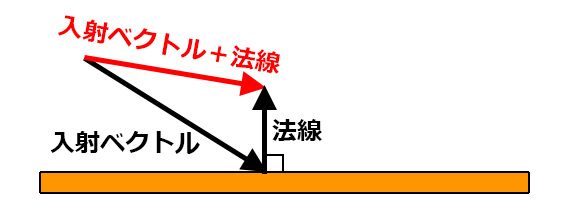
法線が短ければ下を向いたベクトルになる。
そこで都合のいい長さに法線を調整することを考える。
これにはベクトルの内積を利用する。
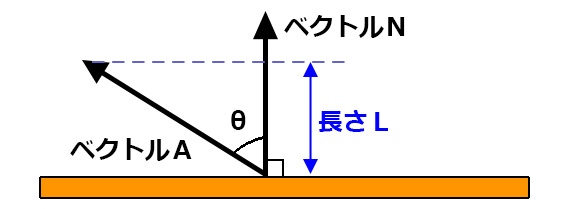
入射ベクトルの逆ベクトルを 、法線を
とした場合、
内積は となるが、
法線の長さは1なので を省いて
となる。
つまり、単純な三角関数を使った計算として長さLが求まる。
このLはベクトルN方向に対するベクトルAの長さ、
いわば真横から光を当てたときの影の長さになるところがポイントだ。
適切な長さに調整した法線を利用する
法線は長さ1なので、好きな値をかけることで
希望の長さに延長・短縮することができる。
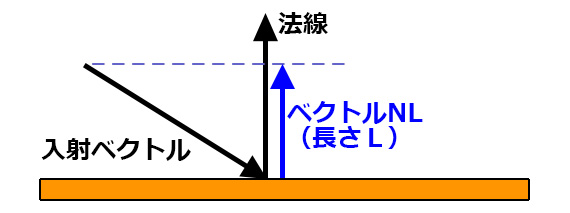
たとえば法線に先ほどのLをかけると
入射ベクトルの影と同じ長さのベクトルNLが作れる。
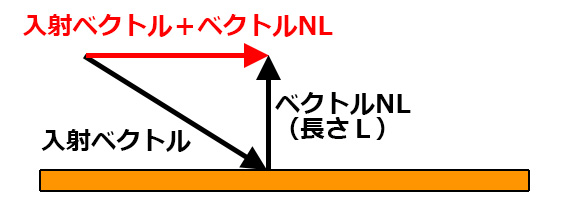
しかしこれを入射ベクトルに足しても
あまり意味のないベクトルになるだけだ。
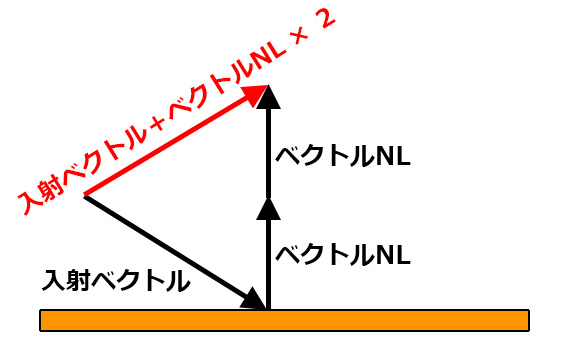
理想的な結果を導くには、入射ベクトルに
ベクトルNLを2本分足すようにする。
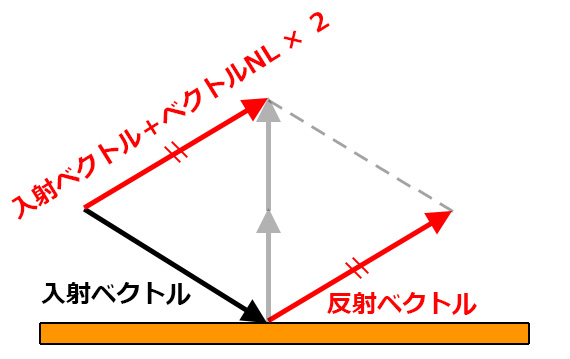
全体をひし形として考えるとわかりやすいが、
「入射ベクトル+ベクトルNL × 2」は
反射ベクトルとそっくり同じ角度・長さなのだ。
つまりこれが衝突面に反射したあとの
新たな移動ベクトルになる。
まとめ
全体の処理をまとめると、
と
の内積
という感じになる。
理屈はややこしく見えるが、
実際の処理は驚くほどシンプルで、
きっちり面の向きに応じた反射が実現できる。