
ゲーム中に出てくる判定や敵AIの処理では
角度の情報が必要になることが多い。
2Dゲームの場合は回転方向が左右しかないので
タンジェントを利用するだけでなんとかなるが、
3Dゲームの場合は横にも縦にも回転できるので
ベクトルの内積を利用する必要が出てくる。
3Dゲーム開発をする上で内積は避けられないため、
早い段階で理解してしまう方がいい。
ベクトルの内積とは
内積の計算には必ず2本のベクトルが関係するので、
ここでは3つの座標のうち2つを結ぶベクトルを考える。
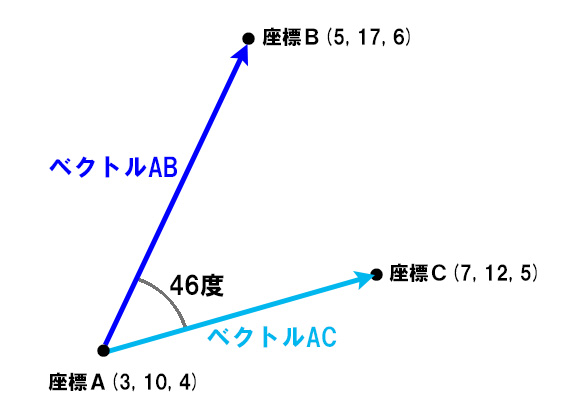
点Aと点Bを結ぶベクトルを 、
点Aと点Cを結ぶベクトルを と表現し、
2本のベクトルの向きは46度ズレているとする。
を求めるには座標Bから座標Aを引き算するだけでいい。
「2ヶ所の座標を引き算すると
その2点を結ぶベクトルが手に入る」
というのはベクトル計算の基本だ。
内積というのは2本のベクトルから求めたひとつの値を指し、
と
の内積は
と表現するが、
この求め方に2種類あるのがミソだ。
内積の計算方法その1
ひとつがベクトルの長さとコサインを利用する方法だ。
は
の長さを表しているので、
上記の式は「 の長さ」と「
の長さ」と「コサインθ」を
すべて掛け合わせた値を求めていることになる。

ベクトルの長さは三平方の定理で求められるので、この図でいえば
となり、コサイン46度は約0.694なので、
それらを踏まえて計算すると
となる。
内積の計算方法その2
もうひとつがベクトルの成分を使う方法だ。
の成分を
、
の成分を
と表現すると、
という計算で内積を求めることができる。

ベクトルの成分というのはXYZ方向それぞれの長さであり、
終点から始点を引き算すればいいので、この図でいえば
となるので、これを踏まえて計算すると
となり、もう一方の計算方法で求めた値と同じ結果になる。
内積の値から角度を求める
さて、内積をうまく利用すると
2本のベクトルの間の角度を求めることができる。
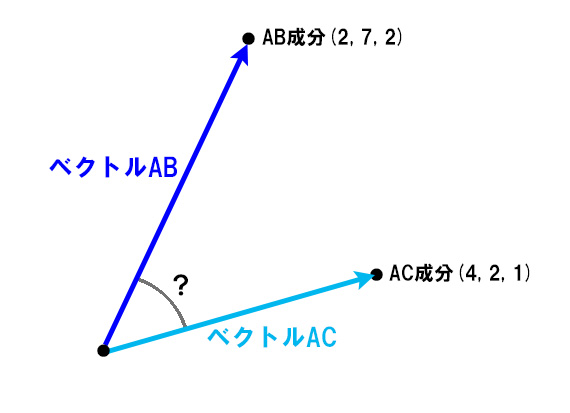
先ほどは角度の値を添えていたが、
実際にはその情報がわからないことが多く、
そこを内積を利用して求めていくのだ。
一旦、内積を求める2つの計算方法を並べてみる。
どちらの計算方法でも同じ値が求まるわけだが、
1つ目の式はベクトルの長さとコサイン値、
2つ目の式はベクトルの成分が必要になる。
ベクトルの成分というのは要するに座標であり、
ゲームプログラムでは必ず保持している情報だ。
つまり、2つ目の式ならいつでも計算できる。
それに対して角度がわからない状況では1つ目の式は使えない。
しかし の計算で求めた内積は
と同じ値なわけだから、角度がわからなくても
「 の長さ」と「
の長さ」と「コサインθ」を
掛け合わせた値を求めることができるということだ。
しかし3つの値を掛け合わせた計算結果から
ひとつの要素だけを取り出すことはできない。
の合計が
だと計算するのは簡単だが、
という値から
や
という値を導き出すのは無理だろう。
つまり の合計がわかっても
そこから角度 を取り出すことはできない。
すべての原因は3つの要素が混ざっているためだ。
そこで と
を
にすることを考える。
ベクトルの向きを変えずに
長さを1にすることを「正規化(せいきか)」と呼ぶが、
ベクトル成分を長さで割るだけで実現できる。
を正規化したものは
と表現する。
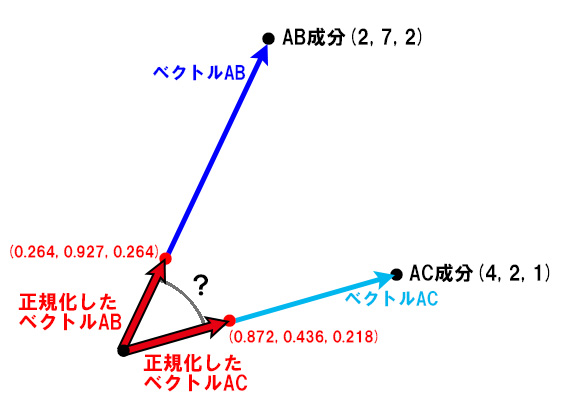
内積を求める式は
だったので、 と
の内積は
となるはずだが、正規化しているため や
は
なので、
となる。
つまり、内積を計算する前に2本のベクトルを正規化しておけば
内積=コサイン値になるわけだ。
角度からコサイン値を求める場合はコサイン関数を使うが、
コサイン値から角度を求める場合は
コサインの逆関数であるアークコサインを使う。
これが内積を使って角度を割り出す仕組みだ。
実際のプログラムではベクトルの正規化も内積の計算も
アークコサインも専用の関数が用意されているので、
自分で計算する必要はまずない。
2本のベクトルを見出せれば角度がわかる
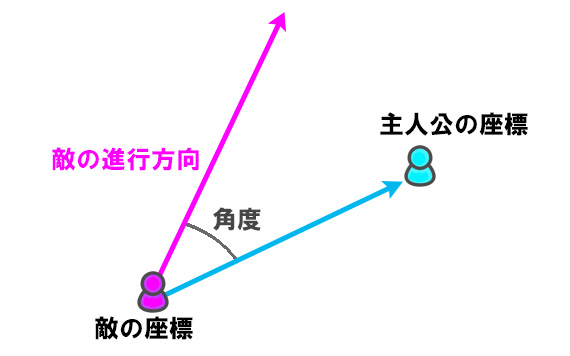
内積を使って角度を求める仕組みさえわかれば
あとは自分が欲しい角度を挟む2本のベクトルを
きちんと見出せるかどうかにかかっている。
敵が攻撃する角度、旋回する方向、画面に表示する方角など
3Dゲームを構成するあらゆる場面で内積が役に立つし、
早めに理解して苦手意識をなくした方が武器になる。