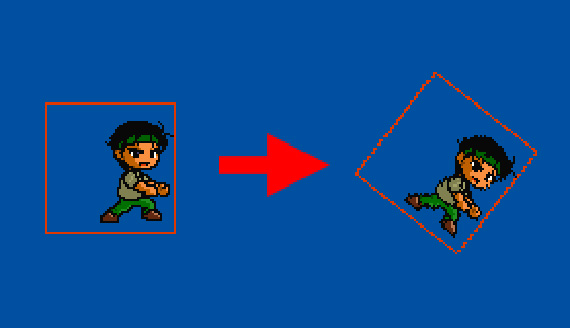
ゲームでの映像表現において
画像の回転処理というのはほぼ必須だが、
昔は画像回転の機能がサポートされていなかった。
しかし吹っ飛ばされるキャラクターや飛び散る破片など
回転を使った方が表現の幅が圧倒的に広がるので、
あらかじめ数度ずつ回転させたグラフィックを作っておくなど
苦肉の策がいろいろと練られた。
とはいえ角度が違うだけの画像を用意するのはデータ容量を食うし、
用意しておいた角度でしか回転できないのも不便。
なんとかリアルタイムに回転処理をしたい。
そこで回転処理を自作してみることにした。

画像というのはピクセルと呼ばれる
色のついた正方形の集まりだ。
これを1ピクセルずつ移動させれば
回転した後の状態が作れるのではないか。
幸いにも点を回転させた場合の座標の求め方は
高校の数学で習ったことがある。
点
を
度回転させた場合の座標
を求める式


上記の に画像を構成するピクセルの位置を当てはめ、
それぞれの回転後の座標に表示してやればいいのだ。
1ピクセルずつ作業していくため
わずか16ピクセル四方の画像でも
16 × 16 = 256回の処理が必要になるが、
画像回転のメリットを考えるとやむを得まい。

と実際にやってみたら画像が穴だらけに。
一応、回転したらしい画像にはなっているものの
これでは使い物にならない。
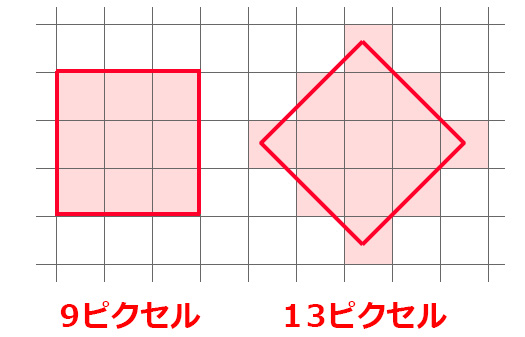
なぜこんな結果になるかというと、
斜め向きの画像であろうが
画面上はあくまで縦横に配置されたピクセルで表現される。
回転していない状態では綺麗に収まっていても
いざ回転すると複数のピクセルにまたがってしまうため、
結果として、元の画像より多いピクセル数が必要なのだ。
また、回転の計算結果は小数を含んだ座標になるが、
ピクセルは整数刻みのため細かい値が切り捨てられる。
その結果、もともと異なる場所にあった2つのピクセルが
同じ位置に来てしまったり、
どのピクセルも移動してこない空白の座標が生まれてしまうのだ。
元の画像のピクセルをひとつずつ移動させるという方法では
回転後に増えるピクセルの分や
空白になってしまうピクセルがどうしても解決できない。
そこで発想を逆転させることにした。
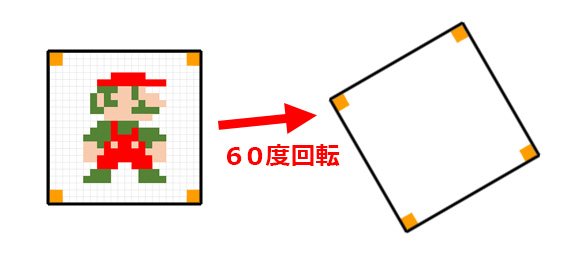
まず、画像の四隅について回転後の座標を求める。
どれほど回転しようが、角にあったピクセルは
回転後も画像の端に位置するはずだ。
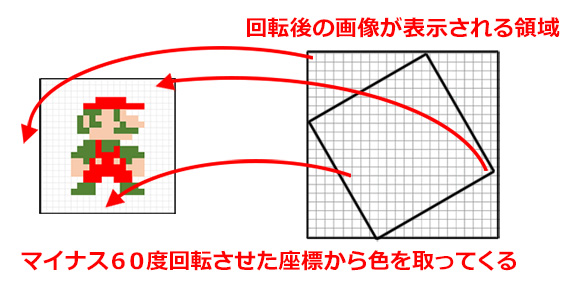
そして画像の端を表す4ヶ所の座標から、
回転後の画像が表示されるであろう領域が判明する。
その領域内のピクセルについて
回転前にどの座標にいたかを求めるのだ。
要するにそれぞれの座標を
角度分だけマイナス方向に回転させればいい。
異なる場所にあるピクセルが
元画像の同じ座標を指し示す場合があるが、
もともと1ピクセルだったものが
複数のピクセルにまたがるのは問題ない。
また、回転前の座標が
元の画像の位置からはみ出す場合は
表示処理をスキップする。
実際には回転する際の原点を調整する処理なども必要だが、
これで抜けのない綺麗な回転画像を作ることができる。
「フロントライン」の初期バージョンは
この処理を使って銃を持った主人公の腕などを回転していた。
サインやコサインといった三角関数が絡む処理になるが、
小数を扱った計算が遅かった当時は
関係する値をあらかじめ数万倍して整数にしておき、
すべての計算を整数同士で行ったあと
最後に割り算して正しい値に戻す、という地味なテクニックもあった。
今となってはこんな苦労をせずに高速な回転処理ができるし、
小数同士の計算に足を引っ張られることもない。
じゃあ当時の苦労は意味がなかったのかというと、
これはこれでいろいろと勉強になったし、
ハードウェア内部でどういう処理をしているかを
知るきっかけにもなったと思う。